Aug 13, · ランベルト正積方位(Lambert azimuthal equalarea)図法 EPSG1027/90などで定義され「(地図中央からの方位と距離が正確な,全体が円形の地図をつくる)正距方位図法の半径方向を圧縮して,正積としたもの」である. 正弦曲線(Sinusoidal)図法9正距方位図法 •図の中心と任意の点との距離と方位が正しい。 長所:図の中心と任意の点とを結ぶ線は 10大圏航路を示し正距である。 →11航空図として利用 短所:面積が正しくない 周辺部の形のひずみが大きい (大圏航路は最短距離である)地図投影法 モード 中学 高校 大学 (地図学) 緯線と経線が直角に交わった地図 面積が正しい地図 中心からの距離と方位が正しい地図 陸が多く見える半球 海が多く見える半球 円筒図法 メルカトル図法正角 メルカトル図法 (太平洋中心)正角
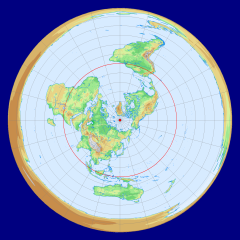
地図投影法学習のための地図画像素材集
正積方位図法 意味
正積方位図法 意味-1 正積図法地球上のどの部分についても、その面積比率が地図上に正しく表現される。 →分布図や密度図など、広がりを示す表現が必要な場合に用いる。 2 おもな正積図法 (1)サンソン図法すべての緯線(直線)と中央経線の長さが正しい。 高緯度地方(周辺部)の歪みが大きい。 ※楕円は、地球上の半径約550kmの円を地図上に描いたもの。 このページの② 等角図法 角または方位を正しく写す ③ 正積図法 面積関係を正しく写す 地図投影法には,地球を直接投影する投射図法,円錐面上に投影してそれを平面上に展開する 円錐図法,また円柱に投影する円柱図法などがある。 (1) 投射図法




正 距 方位 図法
正角図法が用いられている例は,以下のように類別 することが出来よう。(1)各地点における,風 向のよう な方位角を持った量を表現する地図,(2)地点間の方位 を示す図,(3)中大縮尺図,(4)測地測量,(5)正軸法メル カトル図法による航程線の表示。以下ではそれぞれにMay 28, · ランベルト正積方位図法(北極を中心とした地図、北半球のみ)。 極点を中心とした投影は、投影される 扇形 の中心角を360°(すなわち 円板 )に設定した場合の ランベルト正積円錐図法(2)正距方位図法は、緯度・経度が平行にならない。 (3)那覇から北京、仙台の距離は2,000km未満であるが、外務省の地図では2,000km以上になっている。 九州・沖縄サミットのホームページの地図(外務省) 正距方位図法(那覇中心)で作成
ユニバーサル横メルカトル図法では,そのひずみが小さく なるように描かれており,地球と接する経線付近の狭い範囲のみは距離や方位がほぼ正確に描かれる。 国土地理院発行の中縮尺 の地形図(2万5千分の 1地形図や5万分の1地 形図など) 正積図法である。なお,正角図法と正積図法とは矛盾関係 にあり,同時に正角・正積の2条件を満足できな い(野村, 19)。 O どAOB=ζA'O'B' 図5地球上と地図上の角の関係 正lfe 図法 equidistant projection 経線上また は緯線上,あるいは方位線上において長さが正し正積円筒図法の一般論 ランベルト正積方位図法においては、 赤道 付近だけを見れば形が正しい( 正角 である)が、南北に離れるにつれて形が崩れる。 地球上では南北に行くほど経線が狭くなる(緯度 ϕ {\displaystyle \phi \,} に対して cos ϕ {\displaystyle
ランベルト正積方位図法は,1772年に JHLambert が発表した投影法の一つで, 方位図法で正積図法である. まずは,北極を中心とした全球の地図を描いてみよう.J正方位図法の緯線間隔の比較(正軸投影) 平射図法 正距方位図法 n 心射図法 ランベルト正積方位図法 正射図法 メルカトル図法とミラー図法の比較 高緯度地方の拡大を修正 メルカトル図法 ミラー図法 角度が正しい 何も正しくないランベルト正積方位図法 ランベルト正積方位図法としても知られており、1772年にランベルトが有名なBeitrageコレクションの中で発表しました。 この図法は正積で、この特徴に配慮して作成されていますが、透視投影ではありません。 主に、半球の地図や
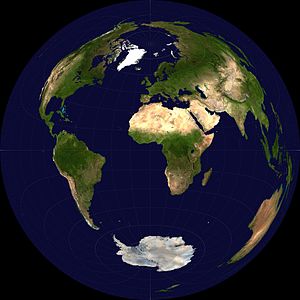



ランベルト正積方位図法 Wikipedia
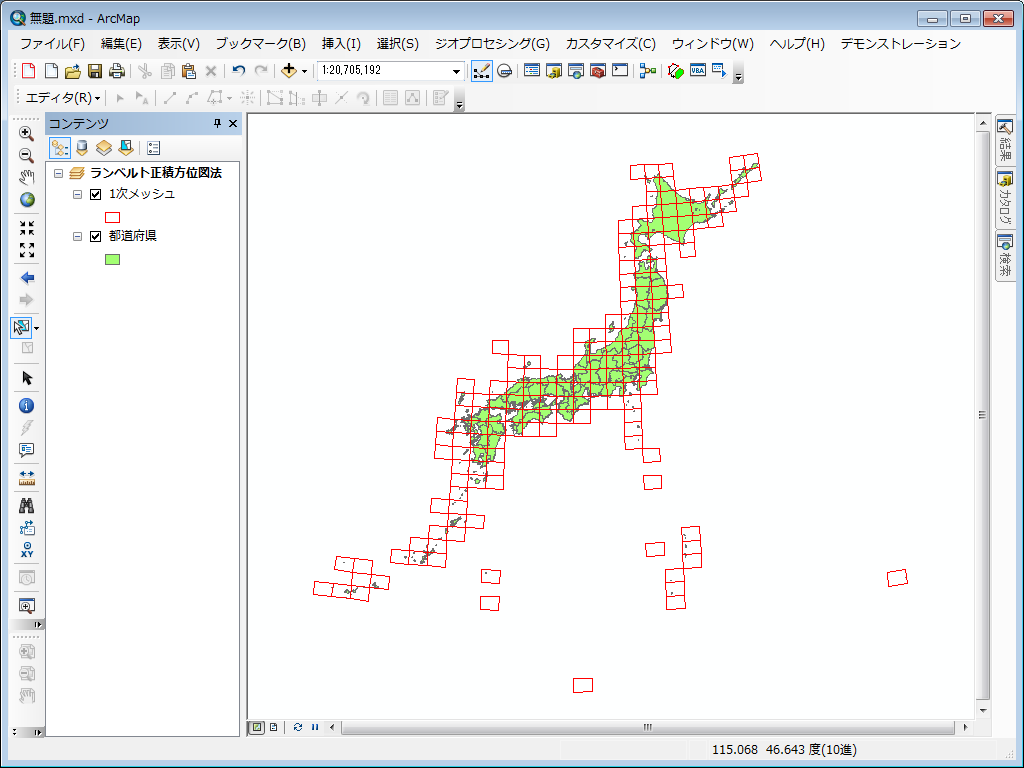



地域メッシュはホントに ほぼ同一の大きさ なのかを調べました Wingfield Since1981
H22年度 測量士補試験 解答 No21No24 地図編集 < No21:地図編集:解答> 解 答 地球表面を平面上に投影して表す地図は、その目的において様々な投影法の選択が行われる。 以下に、各分類法につ投射図法 のほかに, 正積方位図法 , 正距方位図法 が含まれる。 方位図法では,極心法の場合緯線ごとに,その他の場合は地図主点を中心とする同心円ごとに,その上では地図投影のひずみが等しい。 つまり緯線が等ひずみ線となる。 方位図法を変形して,特定の2定点での方向角が正しく表わされるようにした2点等方位図法,またはその2定点から任意の点への正射図法とは、地球を無限遠から平面に投影する方位図法です。 地球を 3 次元に見ているような印象を与えるため、差し込みマップや、宇宙から見た地球を絵画的に表現した地図として使われます。 この地図投影は 局所 投影と同じですが、球体のみを



世界全図 正距方位図法 白地図 の画像素材 地図素材ならイメージナビ




ランベルト正積方位図法 Wikipedia
いちからはじめる gmt その48 jb(アルベルス正積円錐図法) 11年 6月 1日掲載 これまでに,メルカトル図法,正距方位図法,正角円錐図法の 3つの投影法を紹介したが, 今回からは,30種類近くある GMT の投影法の中から, 市販の地図帳に使われている投影ユニバーサル横メルカトル図法では,そのひずみ が小さくなるように描かれており,地球と接する経線付近の狭い範囲のみは距離や方位がほぼ正確に描かれる。 国土地理院発行の中縮尺の地 形図(2万5千分の1地形図 や5万分の1地形図など) 正積図法正積図法せいせきずほうequalarea projection 等積図法ともいい,地球上の 面積 と対応する 地図 上の面積との比 (すなわち 面積縮尺) がどこでもどんな広さでも同じに表わされている 地図投影法 。 地図上の任意の 地点 で特定の2方向の長さが正しく表わされる。 この方向の 包絡線 を等長線という。 方位図法 では (ランベルト) 正積方位図法 ,擬方位図法では ハン
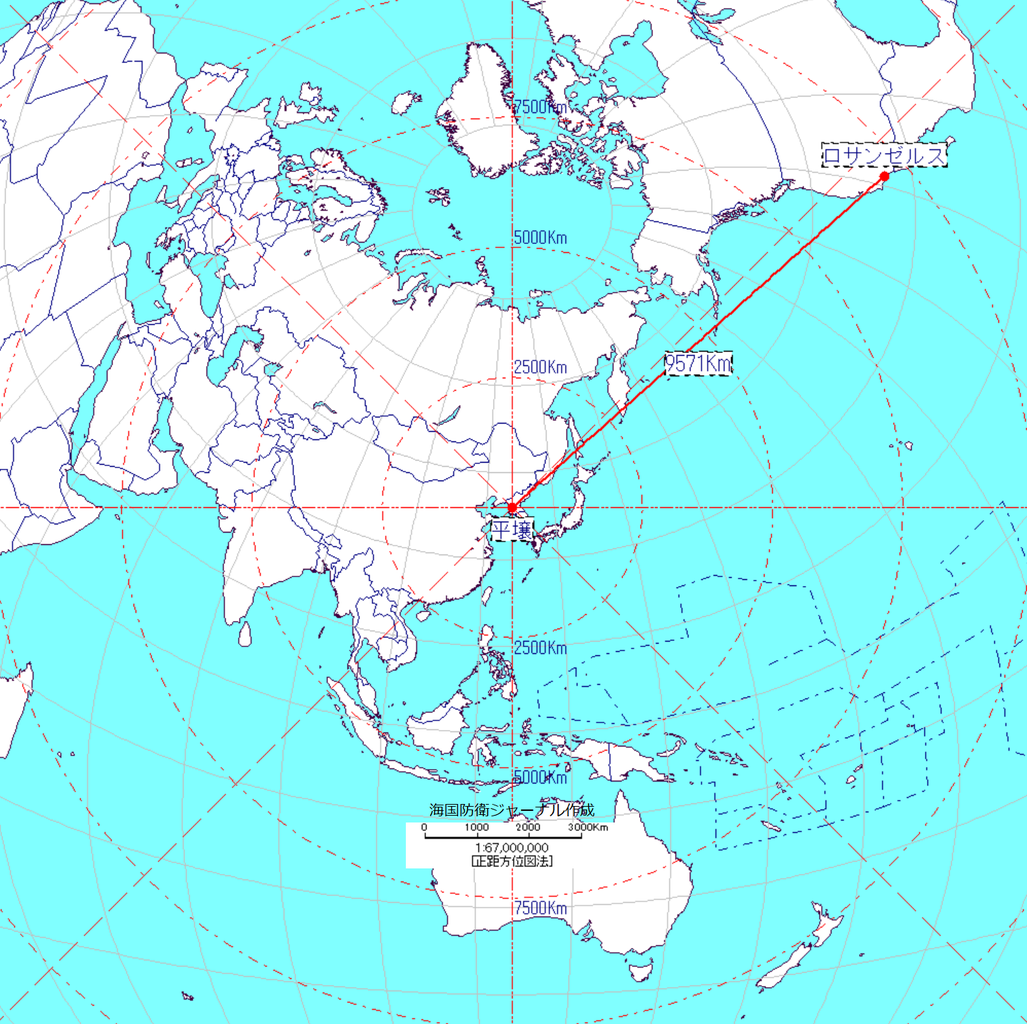



メルカトルの呪い 地図のおはなし 海国防衛ジャーナル




地図投影法学習のための地図画像素材集
ランベルト正積方位法 モデル 正距 タイプ 正積方位 子午線 極:接触点から放射状に広がる直線 斜軸:直線の中央子午線に向かってくぼんだ複合曲線 赤道:直線の中央子午線に向かってくぼんだ複合ランベルト正積方位図法を解説文に含む見出し語の検索結果です。出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 1346 UTC 版)ハンメル図法は、ランベルト正積方位図法を変形して擬円筒図法のような形状にしたものである。ランベルト正積方位図法( Lambert Azimuthal EqualArea Projection ) ランベルト正積方位図法は、地球と一点で接する平面へ地球を投射(一度に投射できるのは地球の半分)するとして、更に投射後の地図上で、地域的な面積の不一致が生じないように補正を加えた地図投影法です。 地球全体(半面)を俯瞰するような地図で多用されています。 ランベルト正積方位図法に



1




正 距 方位 図法
May 15, 19 · 学年 高校全学年, 教科書 新編 詳解地理b改訂版 二宮書店, 単元 地理情報と地図 , キーワード 緯度,経度,地球儀,対蹠点,正積図法,地図投影法,分布図,サンソン図法,モルワイデ図法,グード図法,ホロモサイン図法,ボンヌ図法,中央経線,メルカトル図法,正距方位図法ランベルト正積方位図法は、地形の相対的サイズと中心からの方向の両方を正確に保ちます。 地球上の任意のポイントから平面上に世界が投影されます。 すべての地域 (赤道、極、斜軸) で使用できますが、最もよく使用されるのは極地点です。 この図法は、円形や方形などのように対称的で釣合いのとれた個々の大陸に適しています。 ランベルト正積方位図法は方位角地図は、正積図法、正角図法、正距図法と組み合わせることができます。 方位図法の例として、ランベルト正積方位 (Lambert Equal Area Azimuthal) 図法と正距方位 (Azimuthal Equidistant) 図法




地図投影法 かんたんな説明 球面から平面への投影 地球の表面は球面なのに 紙の地図に 表現する 種々の歪みが生じる 目的に応じて 投影法を考えた 方位を正しく 正方位 角度を正しく 正角 面積を正しく 正積 距離を正しく 正距 地球の表面は球面



地図の投影図法の種類
正距方位図法 » ランベルト正積方位図法 » 横メルカトル図法 » New!大縮尺図法・ 国際横メルカ トル(utm)図 法。 それは, ・メルカトル図法。 ・正距方位図法。 ・ランベルト正積方位図法。 ・多円錐図法。 ・国際横メルカトル図法(大 縮尺,u tm図法)。 の5種 類である。 上記の一覧表は,未 だ完全に整理された内容にはなランベルト方位図法についての詳細 には、0(地理座標系の長半径または半径を使用)、1(短半径または半径を使用)、2(正積半径を計算して使用)、または 3(正積半径を使用し、測地緯度を正積緯度に変換)を指定できます。



応用九星気学 現代風水研究所




ランベルト正積方位図法
正積方位図法 正距方位図法 経緯線を表示 等距離円を表示 回転 ズーム (マウスホイールでも操作可) 静止したときの地図を詳細化しました。 マウスの位置や回転角度によらず、水平方向にドラッグすると東西方向に、垂直方向にドラッグすると南北方向に移動します。 Internet Explorer、Google Chrome、Safariを推奨します。 Firefoxは、Canvas 2Dのpath処理性能が低い投影中心を基準とした地図の回転ができるようになりました URLパラメータで中心位置を指定可能 例:東京中心 正距方位図法 http//wwwflatearthlabcom/WebGL/fullwindowhtml?projCenter=,




ランベルト正積方位図法 Wikipedia




正角図法 Wikipedia




地図投影法学習のための地図画像素材集



いちからはじめる Gmt その49 Ja ランベルト正積方位図法
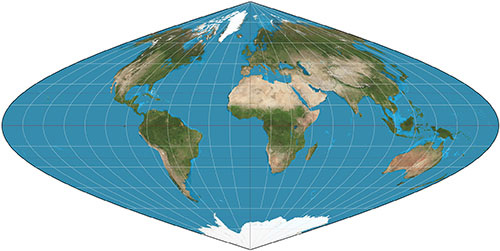



地理 地図の図法




正距方位図法 Azimuthal Equidistant Projection Japaneseclass Jp



1



距離と方位の正しい地図
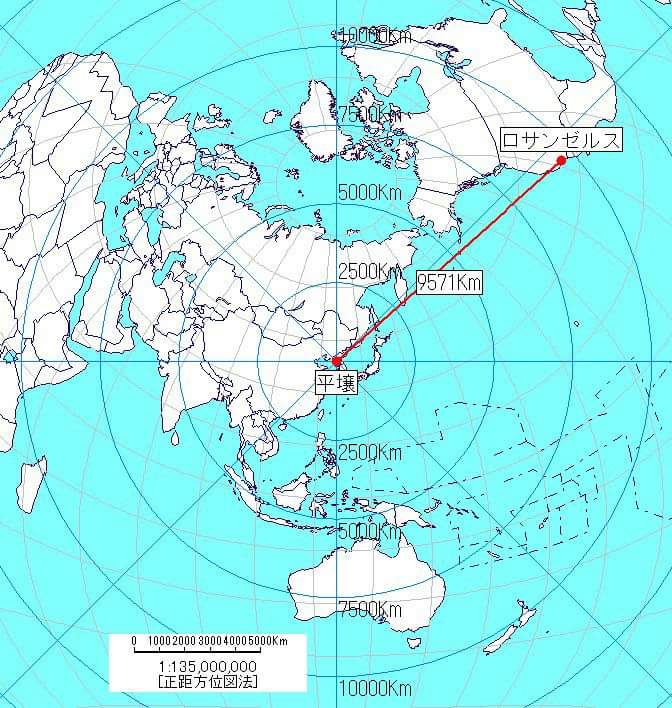



正距方位図法 Twitter Search



地図投影法 投影法カタログ ランベルト正積方位図法
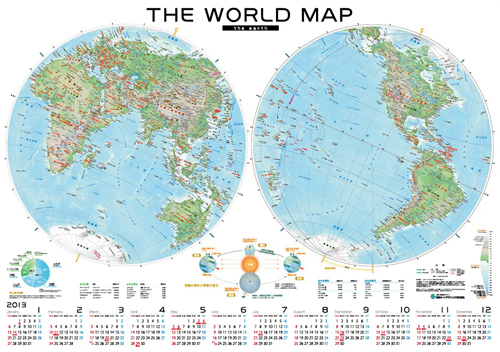



地図のギャラリー 東京カートグラフィック
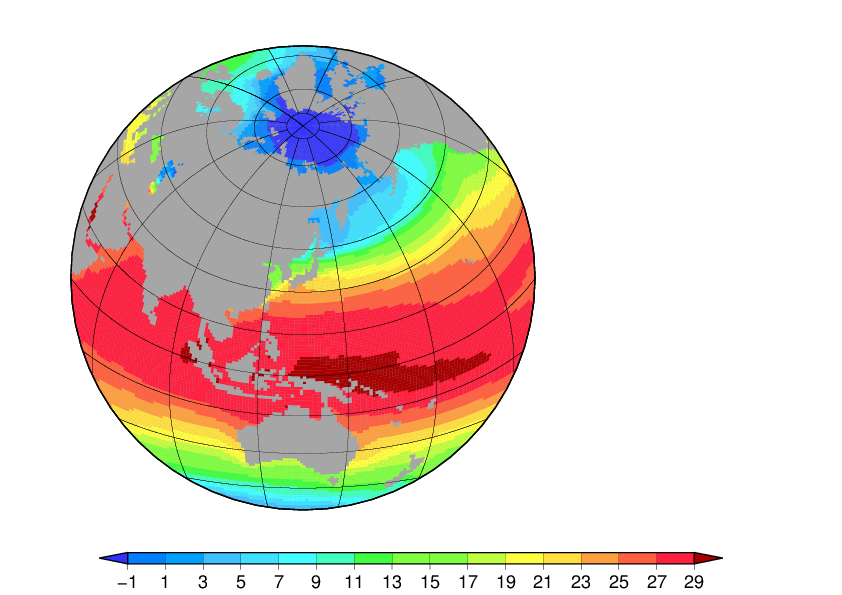



Gmt



方位図法



平凡社地図出版 作品見本 世界
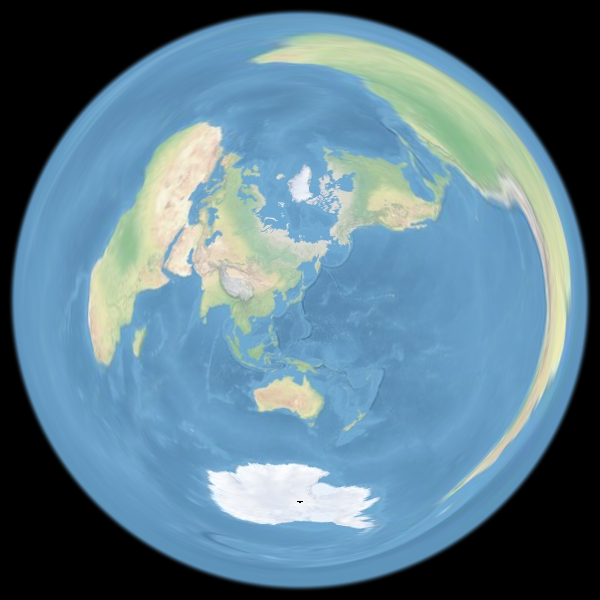



正距方位図法 ランベルト正積方位図法 横メルカトル図法地図




測量に関するミニ知識 国土地理院
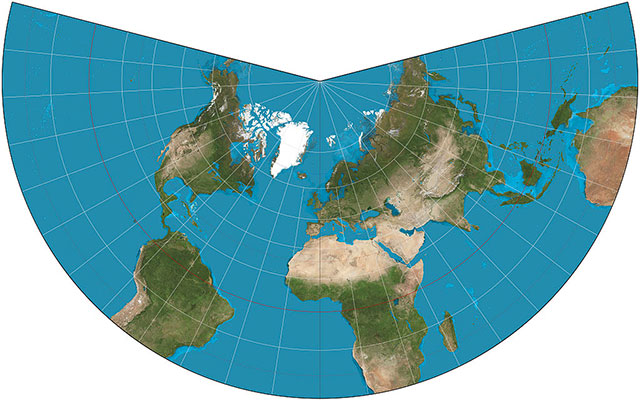



ランベルト正角円錐図法とは コトバンク
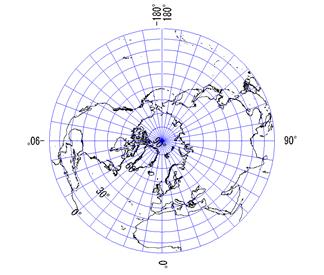



ランベルト正積方位図法 Lambert Azimuthal Equal Area Projection



公孫祐 明鏡止水 地図の図法っていろいろあるんだなぁ 自分が高校行ってた頃に覚えたのは メルカトル図法 モルワイデ図法 正距 方位図法 ぐらいだったような




正距方位図法 Arcmap ドキュメント
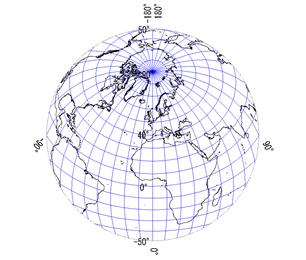



ランベルト正積方位図法 Lambert Azimuthal Equal Area Projection
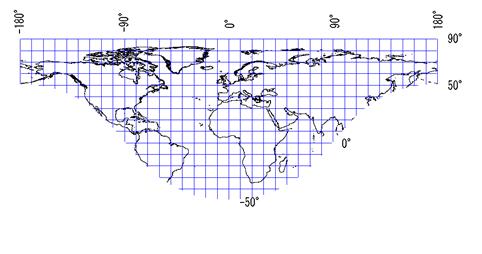



ランベルト正積方位図法 Lambert Azimuthal Equal Area Projection
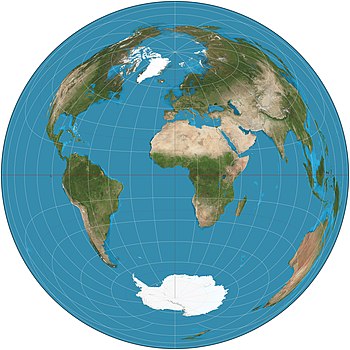



ランバート方位等面積投影 Lambert Azimuthal Equal Area Projection Wikipedia




ランバート方位等面積投影 Lambert Azimuthal Equal Area Projection Wikipedia



世界全図 ランベルト正積方位図法 北極中心 地図素材のダウンロード 日本地図 世界地図 白地図 Mapio




地図投影法学習のための地図画像素材集



世界全図 ランベルト正積方位図法 北極中心 グリーティングカードデザイン素材 おめでた満タン
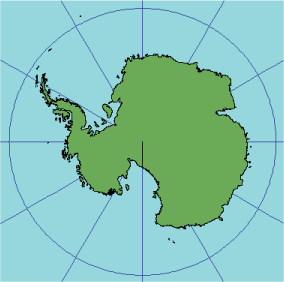



ランベルト正積方位図法 ヘルプ Arcgis For Desktop
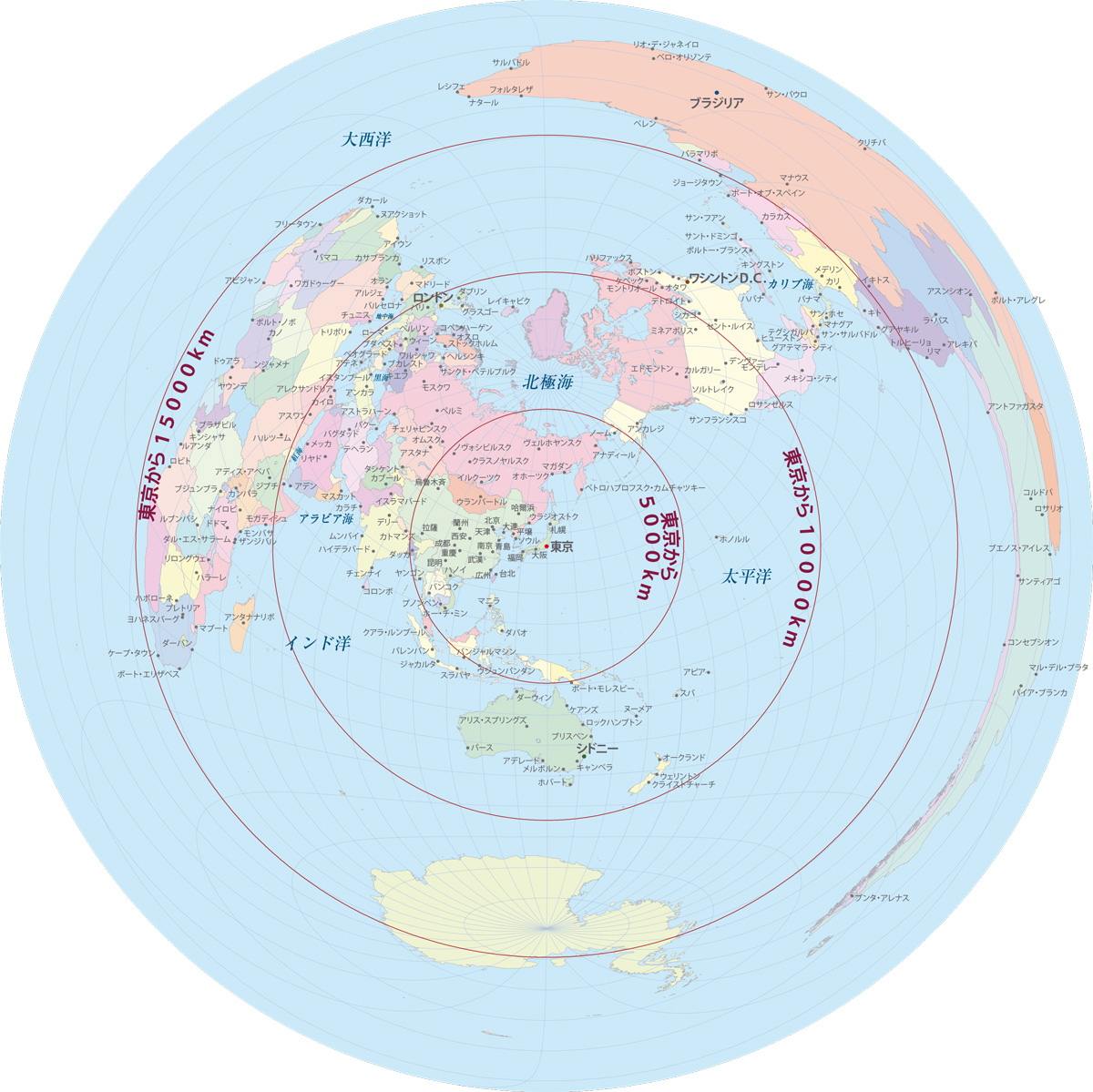



正 距 方位 図法 地図投影法 投影法カタログ 正距方位図法
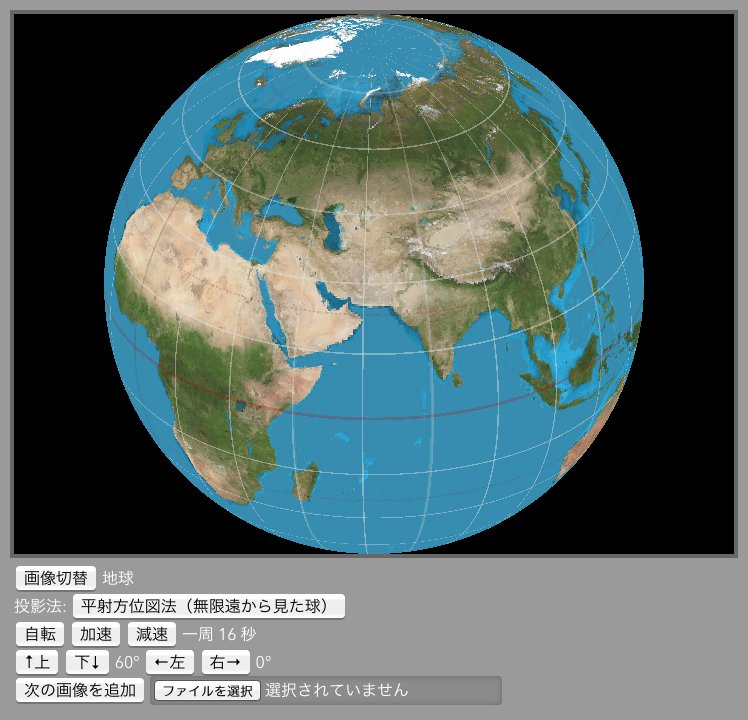



さゆぬ 平射方位図法 正積方位図法 正距方位図法を追加しました 投影法が増えてきて順繰りだと不便なので 取りあえずポップアップメニューにしました
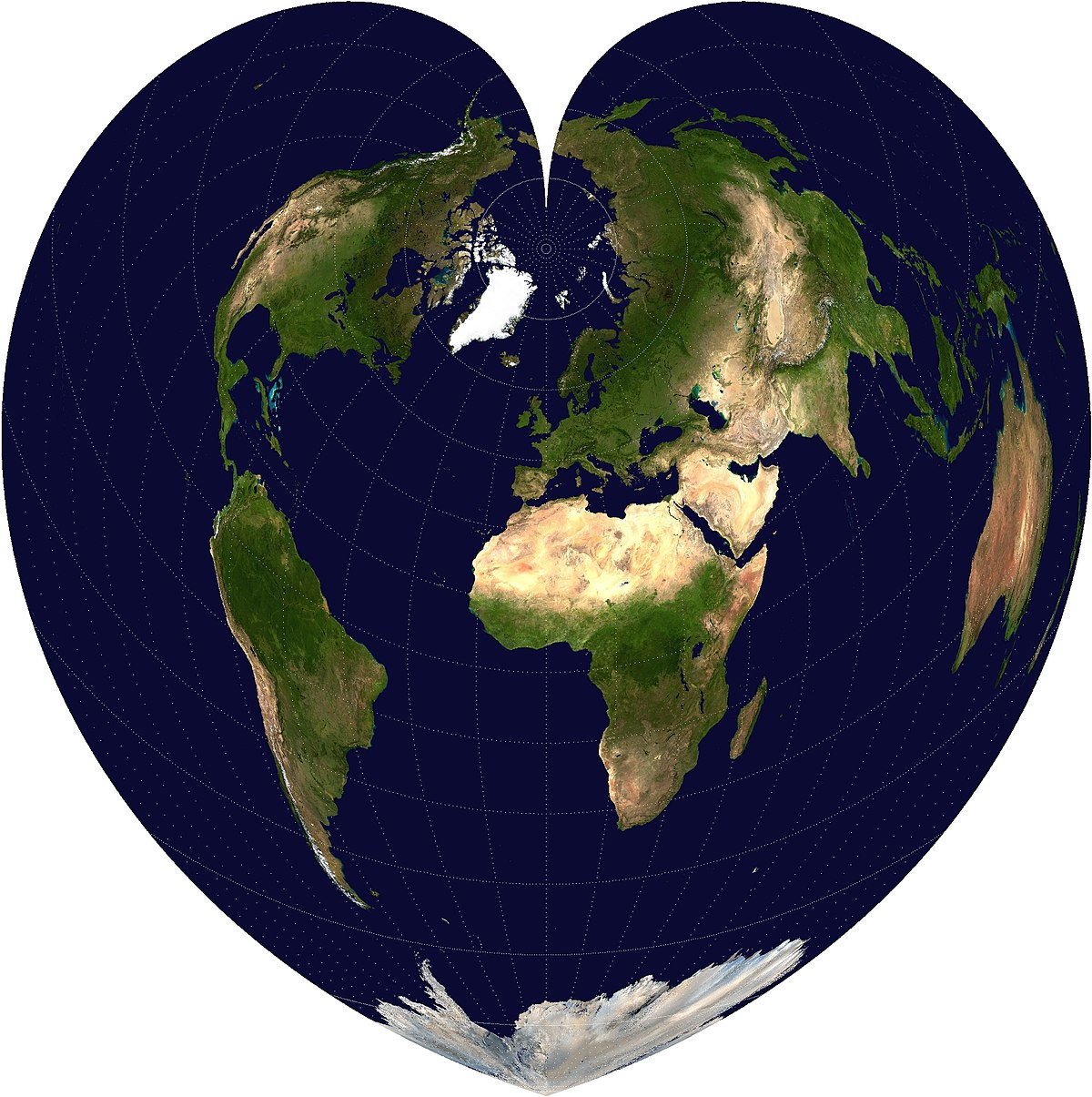



ヴェルナー図法 Wikipedia




正距方位図法 Wikipedia




19時間の大移動 versace ユカリズム
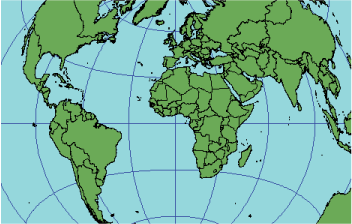



正距方位図法 ヘルプ Arcgis For Desktop
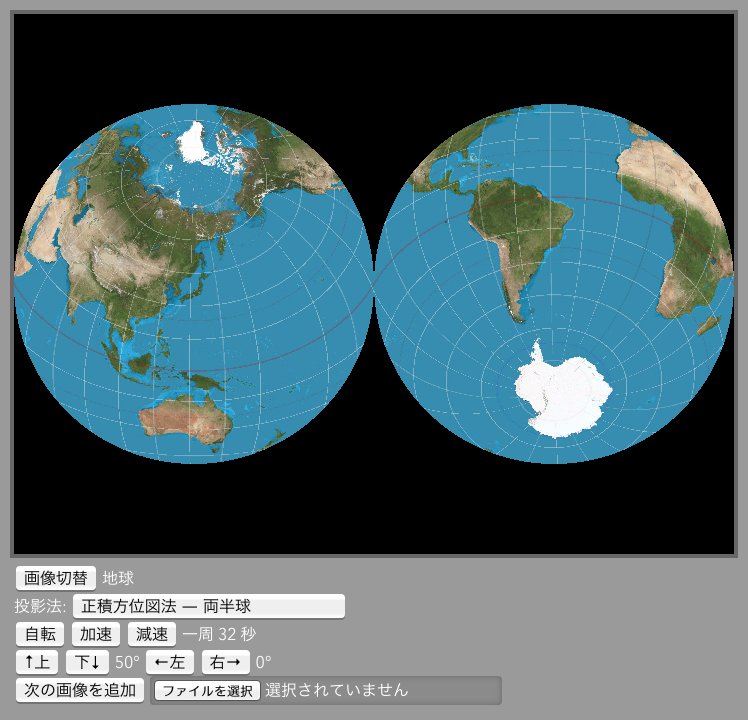



さゆぬ うーむ 投影法 正積円筒図法 0 と 正角円錐図法 45 N を仮に追加しました 円錐図法は Wikipedia の式をコネコネしたら取りあえず逆関数らしき物が出来たけど 縮尺の挙動とかよく分かってない
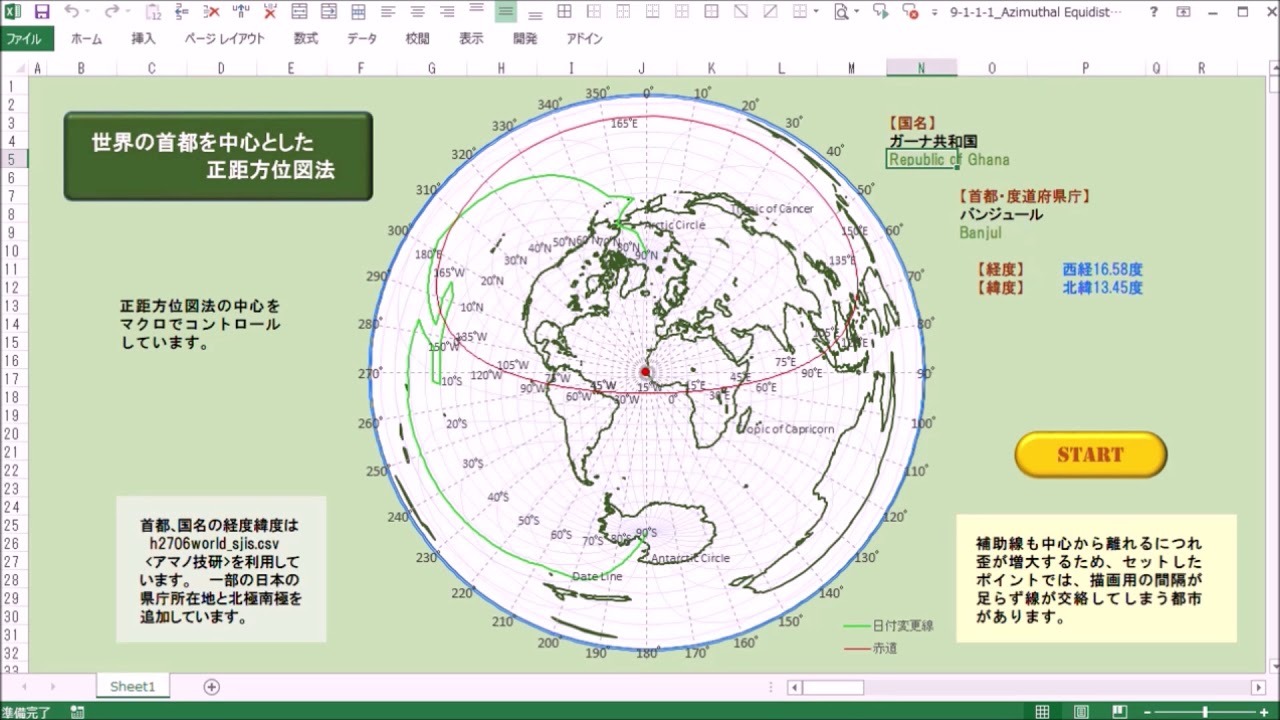



9 1 1 1 正距方位図法 首都 B Youtube




Lambert正積方位図法の写真素材 Fyi ストックフォトのamanaimages Plus
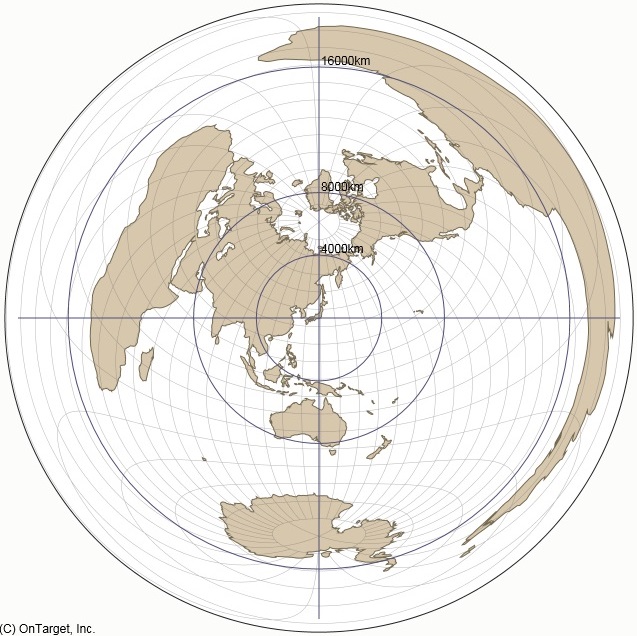



正 距 方位 図法 東京 地図ギャラリー 東京を中心とする世界全図



世界全図 正距方位図法 白地図 の画像素材 地図素材ならイメージナビ




Lambert正積方位図法の写真素材 Fyi ストックフォトのamanaimages Plus
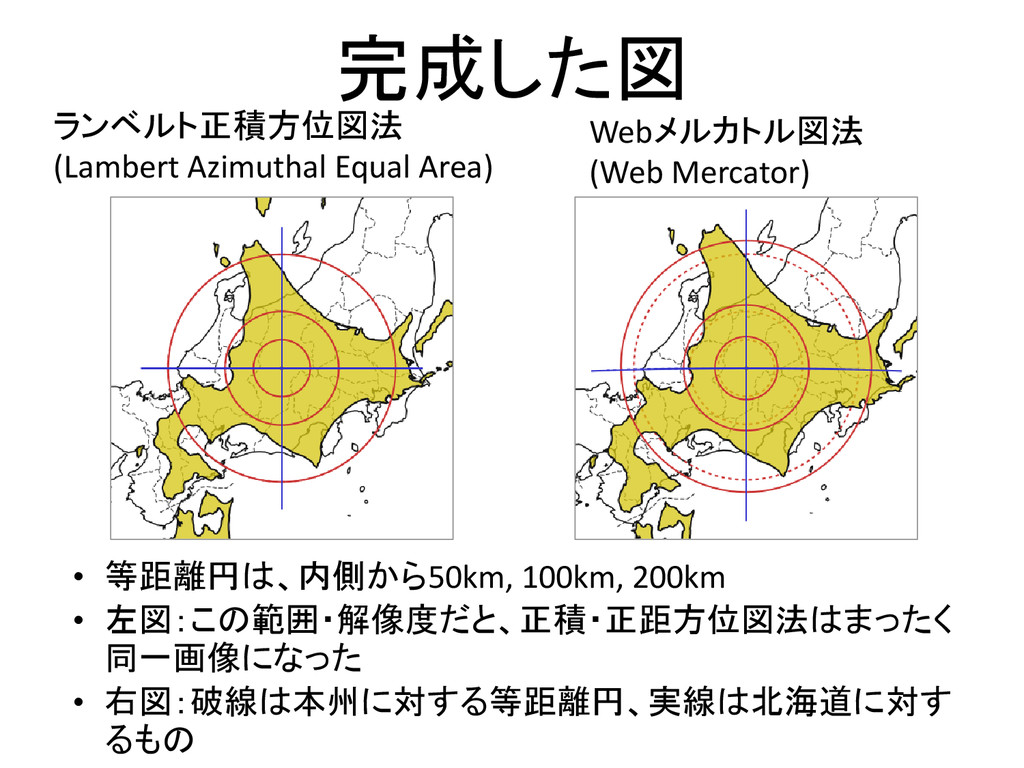



Non Mercator Projection With Mapnik Speaker Deck
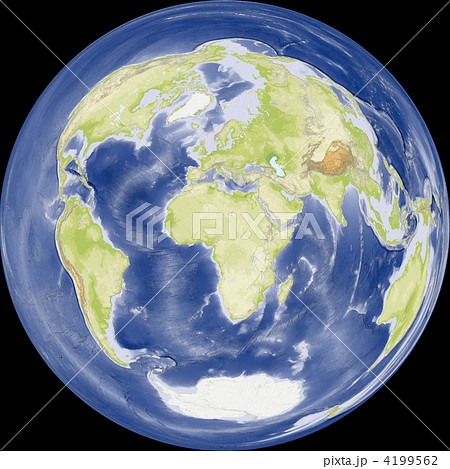



ランベルト正積方位図法のイラスト素材




南アメリカ 陰影図 標高に応じて色 投影ランベルト正積方位図法 60 13extents 107 55 30 18rdata ソース Nasa の写真素材 画像素材 Image




方位図法 Wikipedia
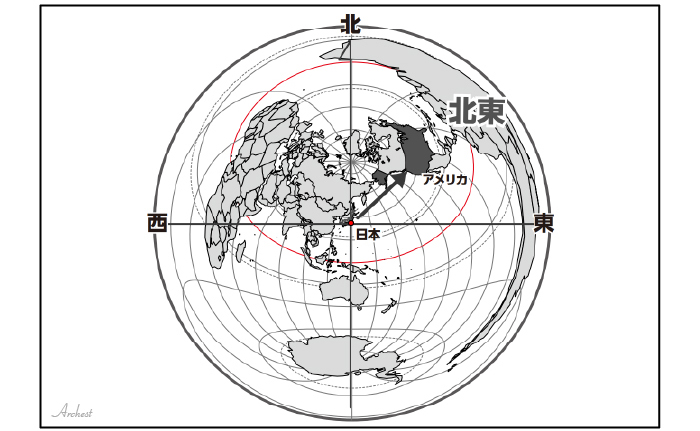



意外と試験に出る 正距正方位図法 の特徴と試験問題攻略法



方位図法



いちからはじめる Gmt その49 Ja ランベルト正積方位図法




正距方位図法 Wikiwand
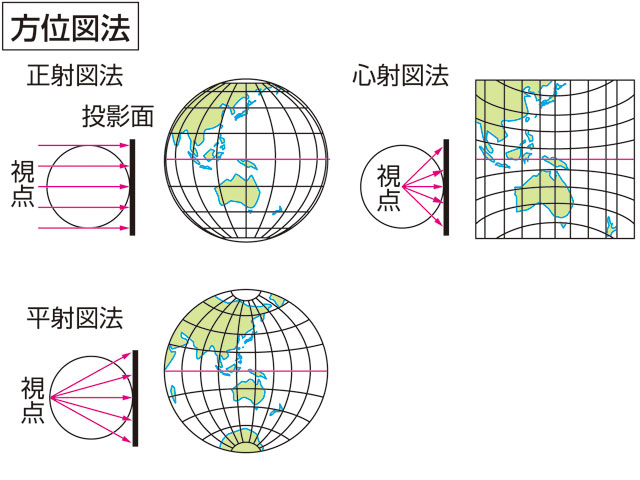



方位図法とは コトバンク




6 5 2 非投射方位図法 珍しい地図が描けます
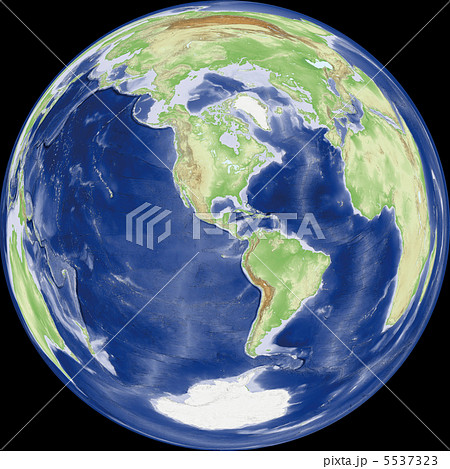



ランベルト正積方位図法のイラスト素材
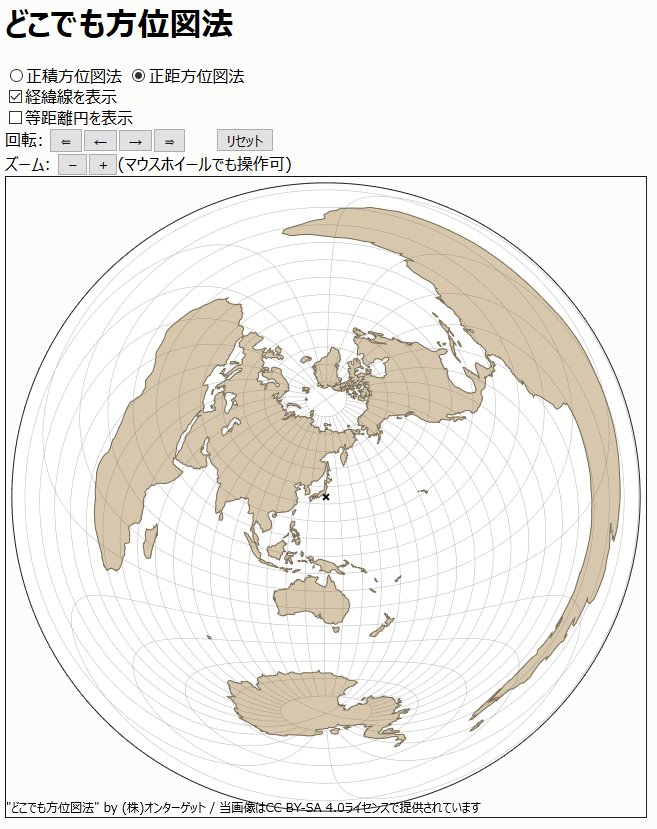



谷謙二 Tani Kenji 正距方位図法 で東京付近を中心にすると 南米大陸は北から東 南東へと変な形になっている 南米は日本の裏側に近いので 少し位置が変わるだけで最短経路も大きく変わってしまい 方位も大きく変わる どこでも方位図法 T Co




ランベルト正距方位図法




Lambert正積方位図法の写真素材 Fyi ストックフォトのamanaimages Plus



地図のギャラリー 東京カートグラフィック



ランベルト正積方位図法 地図のいろいろ



1




ランベルト正積方位図法 Arcgis Pro ドキュメント




ランベルト正積方位法
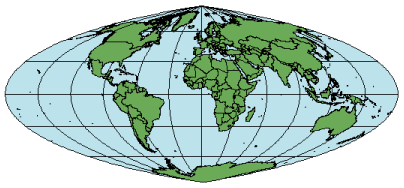



四次正積図法 ヘルプ Arcgis For Desktop



正距方位図法 Wikipedia




吉方位ってどこ Happykeyブログ 開運大作戦
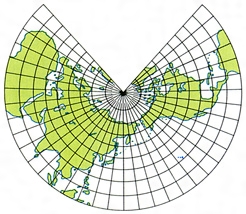



正角円錐図法とは コトバンク



いちからはじめる Gmt その49 Ja ランベルト正積方位図法



世界全図 正距方位図法 白地図 の画像素材 地図素材ならイメージナビ
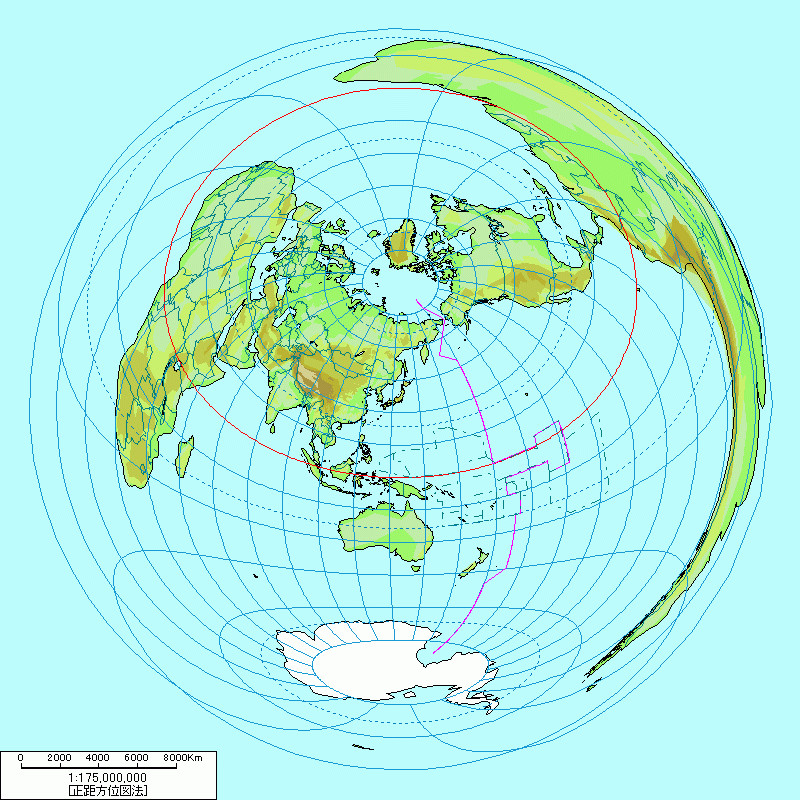



ランベルト正積方位図法 Lambert Azimuthal Equal Area Projection Japaneseclass Jp



世界全図 正距方位図法 行政区分図 の画像素材 地図素材ならイメージナビ
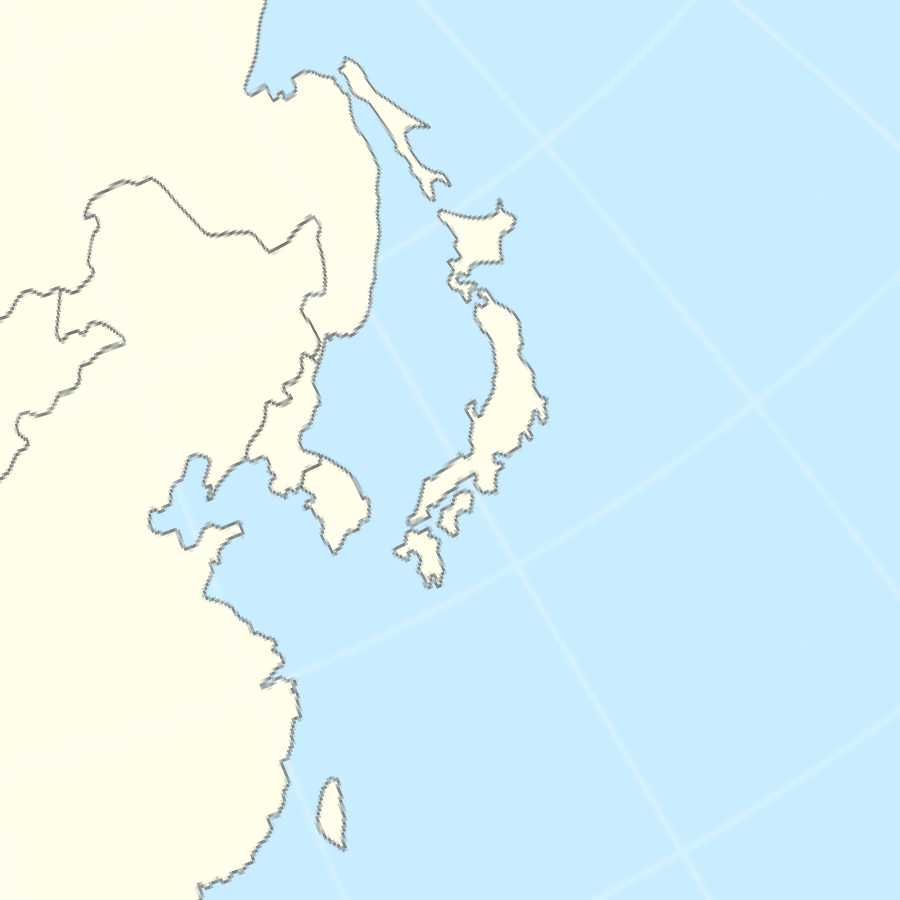



さゆぬ A Twitter チリは意外と太い という話題があったので 日本と同じ条件で投影してみました 同縮尺の正積方位図法でそれぞれ大体中央に配置したので比較できる筈 確かに意外と太い というかでかいなあ
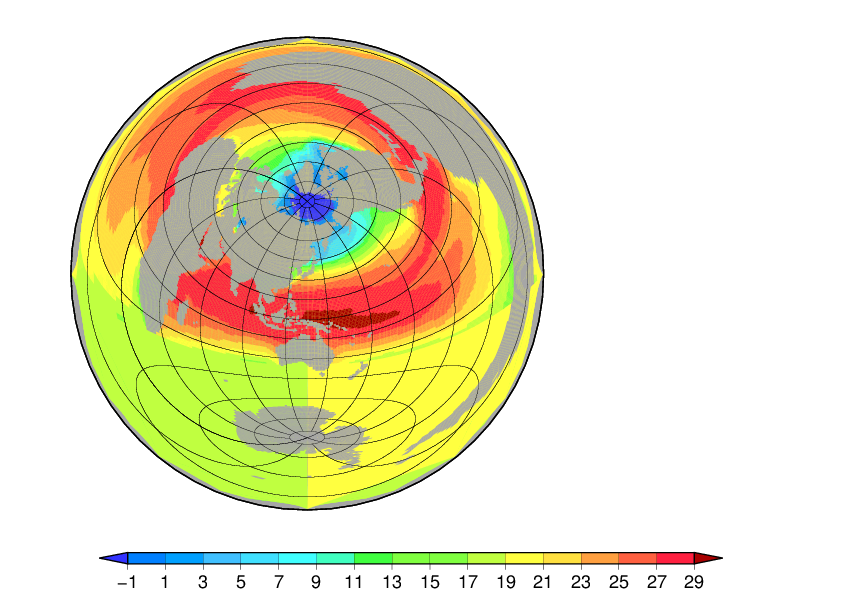



Gmt




南アメリカ 陰影図 植生によると色 投影ランベルト正積方位図法 60 13extents 107 55 30 18rdata ソース Nasa の写真素材 画像素材 Image



世界全図 正距方位図法 地勢図 の画像素材 地図素材ならイメージナビ




Lambert正積方位図法の写真素材 Fyi ストックフォトのamanaimages Plus
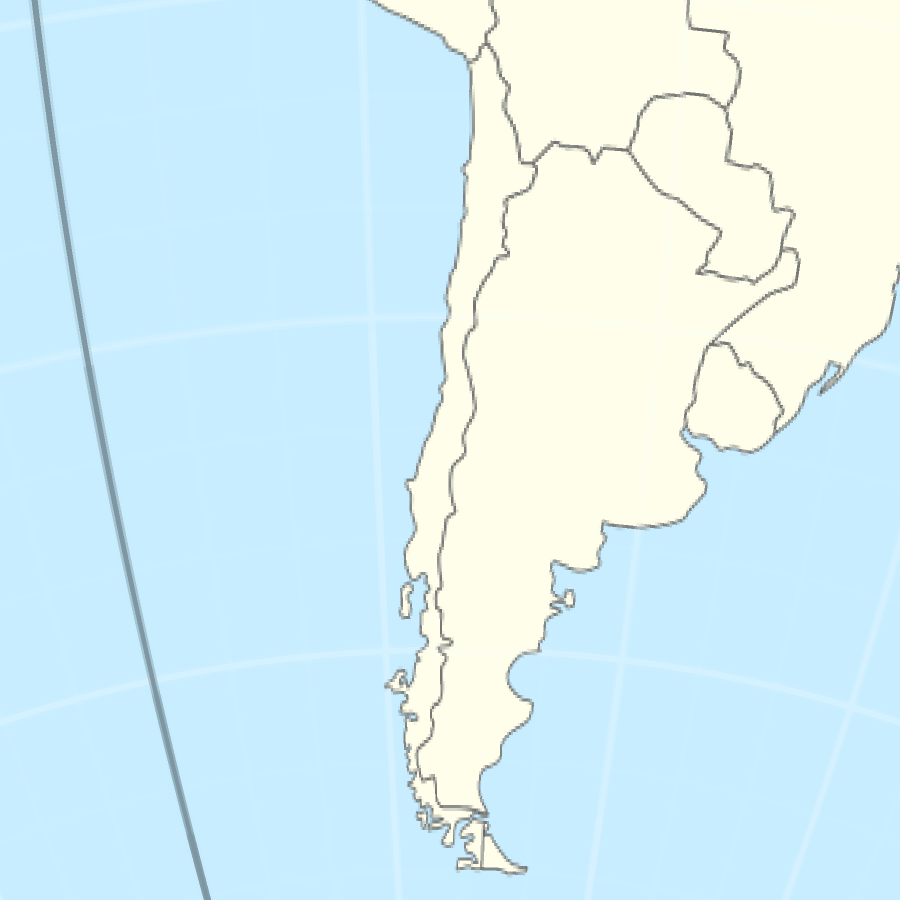



さゆぬ A Twitter チリは意外と太い という話題があったので 日本と同じ条件で投影してみました 同縮尺の正積方位図法でそれぞれ大体中央に配置したので比較できる筈 確かに意外と太い というかでかいなあ



17 8 29に発射された北朝鮮のミサイルはどこを狙っていたのか 生物学博士いいなのぶっちゃけていいっすか



地図投影法学習のための地図画像素材集



平凡社地図出版 作品見本 世界
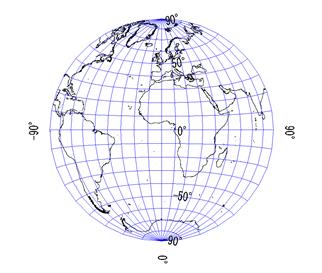



ランベルト正積方位図法 Lambert Azimuthal Equal Area Projection



ランベルト正積方位図法 Lambert Azimuthal Equal Area Projection




地理 地図の図法




正距方位図法 ランベルト正積方位図法 横メルカトル図法地図
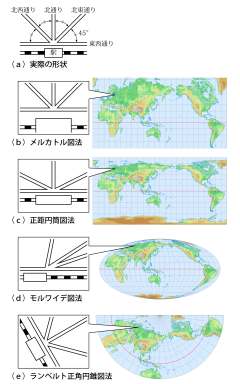



地図投影法学習のための地図画像素材集
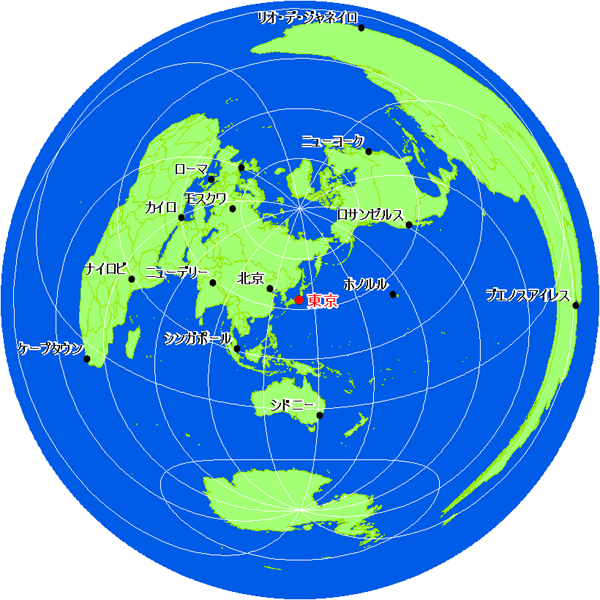



地図についてのよくある勘違い 正距方位図法による世界地図 地理バカ日誌 地図の園




Lambert正積方位図法の写真素材 Fyi ストックフォトのamanaimages Plus
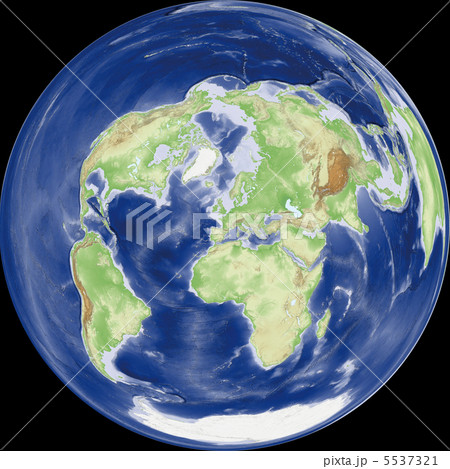



ランベルト正積方位図法のイラスト素材




第3章 空間データの変換と管理 1 空間データの変換 Ppt Download



方位と地図のまとめ 中級篇



正積図法 正角図法 正距方位図法の用途をそれぞれ教えてください と関 Yahoo 知恵袋




ランベルト正角円錐図法




どうでも良い事ですが ミサイルの蘊蓄にお勧めのどこでも方位図法 夢老い人の呟き



3



地図投影法 投影法の分類 正性質



地図の投影図法の種類


0 件のコメント:
コメントを投稿